WEB TUTORIAL - Group Theory
Interpreting Results
Now that the Reduction Forumla has given us the A1g, B1g, Eg, A2u, B2u and A2g representations, we have to check the Character Table for Normal and Quadratic Terms to determine whether the representations will be IR or Raman active.
| D4h | E | 2C4 (z) | C2 | 2C'2 | 2C''2 | i | 2S4 | 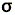 h h |
2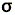 v v |
2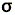 d d |
Rotations |
Functions |
Functions |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1g | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | - | x2+y2, z2 | - |
| A2g | +1 | +1 | +1 | -1 | -1 | +1 | +1 | +1 | -1 | -1 | Rz | - | - |
| B1g | +1 | -1 | +1 | +1 | -1 | +1 | -1 | +1 | +1 | -1 | - | x2-y2 | - |
| B2g | +1 | -1 | +1 | -1 | +1 | +1 | -1 | +1 | -1 | +1 | - | xy | - |
| Eg | +2 | 0 | -2 | 0 | 0 | +2 | 0 | -2 | 0 | 0 | (Rx, Ry) | (xz, yz) | - |
| A1u | +1 | +1 | +1 | +1 | +1 | -1 | -1 | -1 | -1 | -1 | - | - | - |
| A2u | +1 | +1 | +1 | -1 | -1 | -1 | -1 | -1 | +1 | +1 | z | - | z3, z(x2+y2) |
| B1u | +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | -1 | +1 | - | - | xyz |
| B2u | +1 | -1 | +1 | -1 | +1 | -1 | +1 | -1 | +1 | -1 | - | - | z(x2-y2) |
| Eu | +2 | 0 | -2 | 0 | 0 | -2 | 0 | +2 | 0 | 0 | (x, y) | - | (xz2, yz2) (xy2, x2y), (x3, y3) |
h = 16
From this we see that they are both IR and Raman active. This is reported as below:
Ignoring Eg, we will therefore expect to see 2 bands in the IR spectra of [Re2Cl8]2-, and 2 in the Raman spectra. But what about Eg - Should we expect it to result in an additional band in the IR and Raman spectra, or just as an additional band in the IR spectra, or just as an additional band in the Raman spectra?
WELL DONE! You have now completed the Group Theory tutorial! If you have any issues please use the Help Pages or return to Home.